Introduction

Physics attempts to speak about aspects of the real world, using precise mathematical language. We want such a language for:

• Classical Mechanics

• Electromagnetism

• Quantum Mechanics

• Statistical Physics

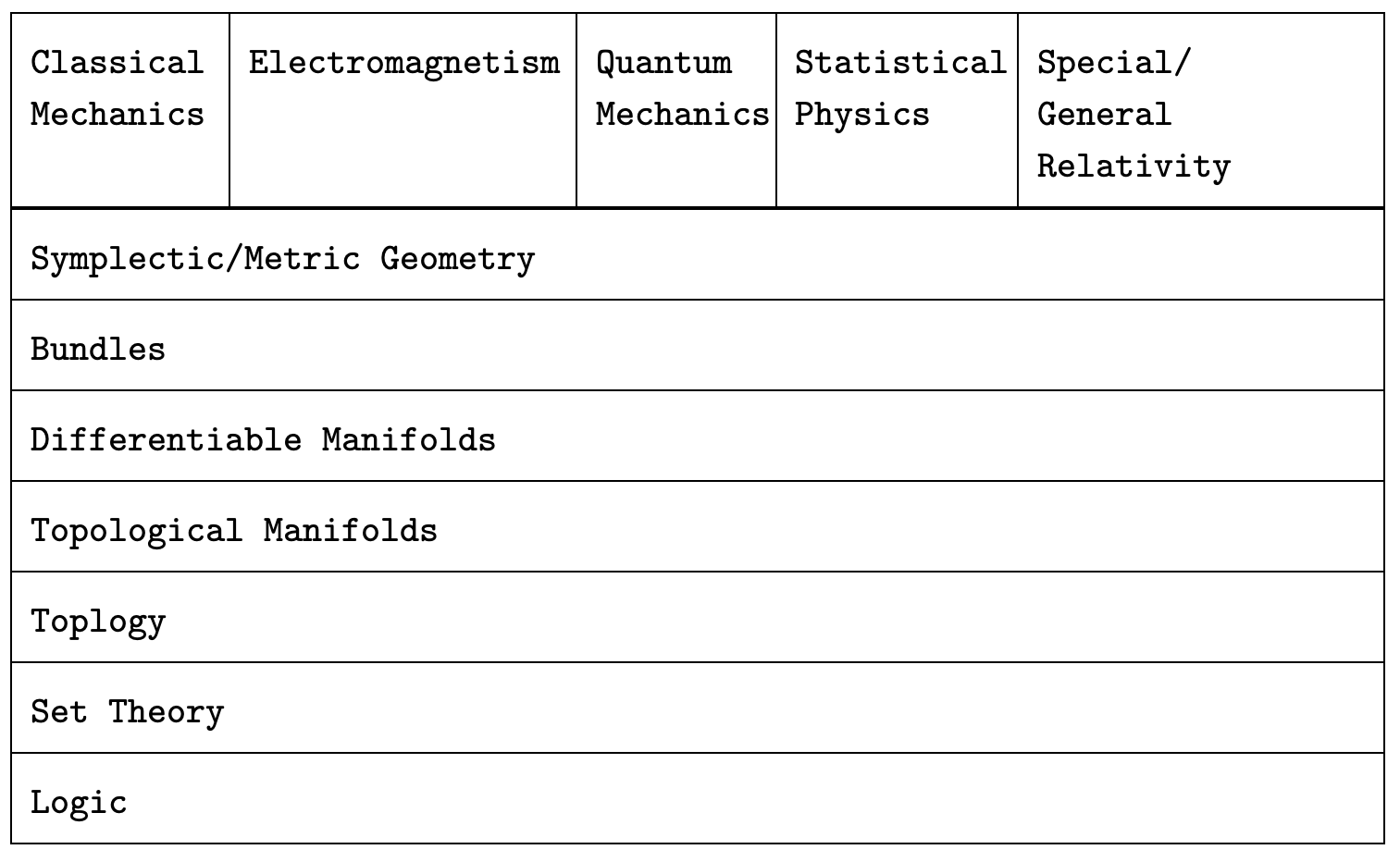
Up to this point, the study of these subjects requires Analysis, Algebra and Geometry.

• Analysis/Geometry: Classical Mechanics, Electrodynamics, General Relativity.

• Analysis/ Algebra (Functional Analysis: Quantum Mechanics.

• Algebra/Geometry: Statistical Physics.

• Analysis/Algebra/Geometry: Differential Geometry.

The general structure of this anatomy:

Propositional Logic.

Def. The fundamental concept is a proposition: a variable that can take on the values true, or false. PL is responsible for deciding the truth value of a proposition, and thus deals with the whole thing, under the assumption that it is true or false.

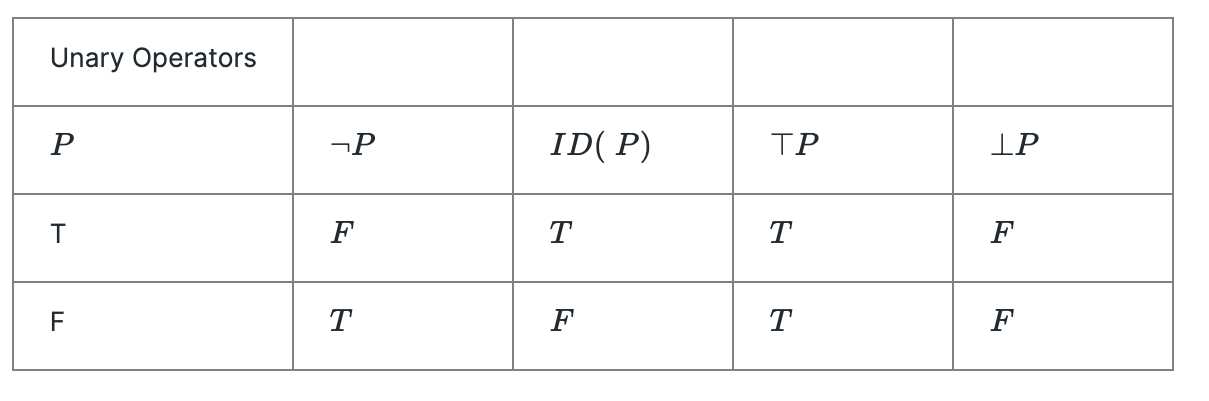
Def. A proposition which always true is a tautology, a proposition which is always false is a contradiction. We can build new propositions, out of old propositions, using logical operators, the simplest of which are unary, and consume one proposition, to return another.

Unary & Binary Operators:

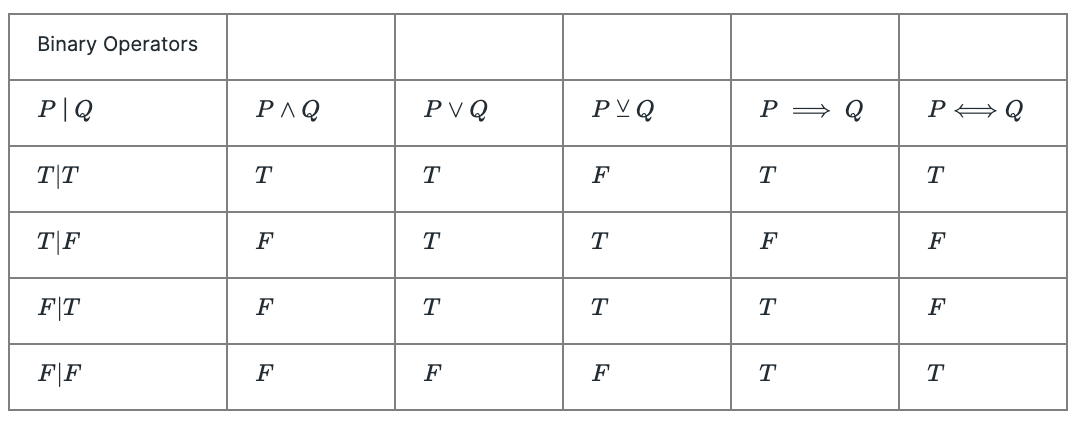
The binary operator for implication, is tricky: the reason that false can imply true is based on the latin phrase, "ex falso quod libet", which means from false assumptions, anything follows, and the mathematical benefit is that this definition, unlocks proof by contradiction, as: $\\P \implies Q \leftrightarrow \neg Q \implies \neg P$.

Theorem: Let $p,q$ be propositions. Then: $\\ (p \implies q) \Longleftrightarrow ((\neg q) \Longrightarrow (\neg p))$

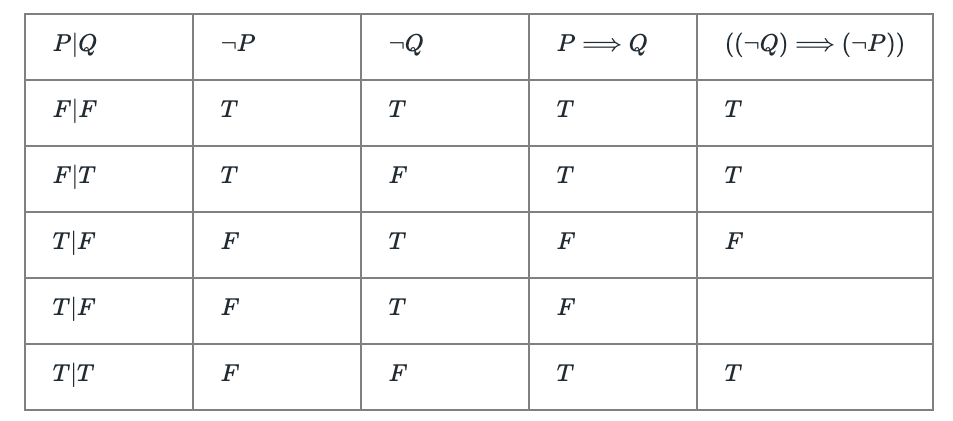
$\text{Remark}\;1$: With these operators, we agree on the decreasing binding strength of the operators in the following sequence: $\neg, \land, \lor, \implies, \Longleftrightarrow$.

$\text{Remark}\; 2$: All higher order operators, of the form $\sigma(p_1,...,P_n)$, can be constructed from the nand operator, denoted: ($\barwedge$).

Predicate Logic.

Def. The fundamental concept, a predicate, informally, is a proposition valued function of some variable(s). For instance $P(x)$ is true or false depending on x.

Def. A predicate of two variables is a relation.

$P(x)$ is a proposition for choices of $x$, and similarly $Q(x, y)$ is such a proposition with a truth value dependent on $x$, and $y$. Predicate logic doesn't examine how predicates are composed, as that requires language for establishing the rules for combining $x$ and $y$ into a predicate. We also do not specify which set they come from, as we're building up to define the set as a concept, and thus can't make use of it prior.

We can still build predicates from given ones, i.e $Q(x,y,z): \Longleftrightarrow P(x) \land R(y,z)$, and we can construct new propositions from predicates using quantifiers.

Quantifiers:

Def. Universal Quantifier ($\forall$):

Def. Let $P(x)$ be a predicate. Then $\forall x : P(x)$, and this is defined to be true if $P(x)$ is true independent of $x$.

Def. Existential Quantifier: ($\exists$):

Let $P(x)$ be a predicate. Then $\exists x : P(x) :\Longleftrightarrow \neg (\forall x : \neg P(x))$

Corollary: $\forall x : P(x) \Longleftrightarrow \neg (\exists x : P(x))$.

If, for every $x$, it is true that $x$ has some property, then it must not be true that there exists an $x$ which doesn't.

$\text{Remark}\;1$: Quantification allows for predicates of multiple variables: Given some predicate $P(x,y)$, then for fixed values of $y, P(x,y)$ is a predicate of one variable, and we define $Q(y) : \Longleftrightarrow \forall x : P(x, y)$. Now we can define $\\ \exists y: \forall x : P(x, y) :\Longleftrightarrow \exists y : Q(y)$

Here, $y$ is a bound variable, and $x$ is free.

$\text{Remark}\;2$: Order matters. $\forall x : \exists y: P(x,y)$ is generically different from $\exists y : \forall x : P(x,y)$.

Consider the proposition expressing the existence of additive inverses in $\mathbb{R}$:

$\forall x : \exists y : x + y = 0$.

This states that for each $x$, there exists a $y$, such that $x+y=0$, or $-x$. If we swap the quantifiers, i.e $\exists y: \forall x : x + y = 0$, what we're saying that for every $x$, there is a $y$ such that $x+y=0$, which is actually false, as if $x + y = 0, (x+1) + y \neq 0$, meaning one $y$ can't work for even two $x$'s, let alone every one.

Axiomatic Systems & Theory of Proofs.

Def. An axiomatic system is a finite sequence of propositions $a_1, a_2,..., a_n$, called axioms.

Def. A proof of a proposition in an axiomatic system $a_1, a_2,..., a_n$, is a finite sequence of propositions $q_1,q_2,...,q_n$, such that for any $1 \leq j \leq M$, either:

(A) $q_j$ is a proposition from the list of axioms.

(T) $q_j$ is a tautology (always true).

(M) $\exists 1 \leq m,n \lt j : (q_m \land q_n \implies q_j)$ is true.

If proposition $\mathcal{P}$ is provable within the system, $a_1, \ldots, a_n$, we say $a_1, \ldots, a_n \vdash \mathcal{P}$, or this sequence proves $\mathcal{P}$.

Consistency of axiomatic systems depends on there being propositions that weren't provable in the system, due to the issue of ex falso quodlibet, which allows us to prove anything, given the right false starting point, and the fact that things aren't provable relies on there being no contradictory axioms.