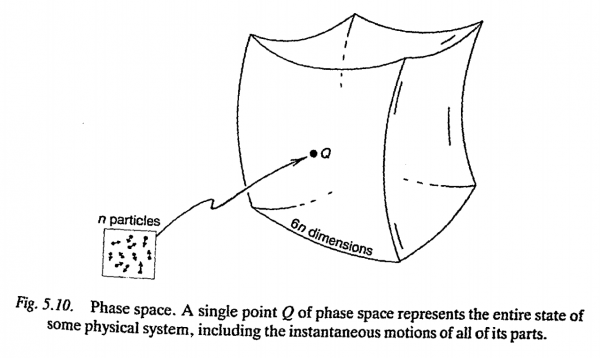
[[Topology vs. Geometry]] Abstract: This paper will attempt to put forth a set of conditions from which an indication that the structures required to describe space time at the Planck scale are topological, not geometrical, can be drawn. Introduction This paper is related to a project, which desires to find the minimal set of assumptions from which the basic theories of physics can be derived. In physics, topology captures what is experimentally verifiable (logically sound/well founded). The fact that a continuous quantity has a precise value is not an experimentally verifiable fact. This clarifies a division between topology, and geometry- topological constructs are more primitive than geometrical ones because they have no idea of size. I would assume this has something to do with the fact that geometry is tied to Euclidean space, because the 3rd spatial dimension (width) is necessary for something to have size as we think about it. What's odd for me is not so much the concept of a sizeless square of infinite length and height in 2D space, but the idea that, "reality" was at some point 2D. how?! I suppose [[anyons]] might shed some light on this. This means prior to assessing the distance between points, we must distinguish them- this insight helps understand how different topologically equivalent sections of space, can have different [[Riemannian]] geometry. On [[Phase Space]], within a singular dimension, units of position, cannot be compared to units of momentum. A [[Phase Space]] is a mathematical tool that allows us to grasp important aspects of complicated systems. - [[Physics Travel Guide]].

Before we assess whether space-time is a geometrically Riemannian manifold, we need to understand whether space-time is topologically a manifold. ^^A manifold, is a set of possible cases {$X...$}, that can be mapped onto a set of real values.^^ So, one question is, when can a set of possibilities, be experimentally identified by a set of real values? This leads us to a rephrasing of the question: When are the cases we want to distinguish parameterized by the real line? - Assuming real line refers to $\mathbb R$, are we asking when each of the possibility variables can be mapped onto the real line? - Perhaps, given $\mathbb R$, could there be a possibility that we can verify, by replacing its parameters with "arguments" that exist on the real line? Since space-time in relativity is four dimensional, it would seem like we're ignoring the most interesting cases, by excluding higher dimensional spaces, but the issue here is time- we must be able to use the time coordinate as the affine (allowing for the preservation or existence of parallel relationships) parameter for the evolution of a particle: $x^{i} = x^{i}(x^{0})$. Functions must be topologically continuous, to avoid breaking experimental verifiability (the mapping of one set of verifiable statements to another). Because we are including the evolution of time, the topology we give time, will be a major constraint on the topology of the space in which it the evolution will occur. Furthermore, the reverse argument is true as well: the topology we give space, must be the same as the one given to time, because spatial distance, can be used as a time parameter, i.e. two ships drifting at constant velocity can use the distance between them as a clock. Clock Condition For any events $a, b:$ $if\; a ->\; b,\; then\; C_i\langle a \rangle\preccurlyeq C_i\langle b \rangle$ If a implies b (or if b can be derived from a), then the Clock Condition of event a should should be $lt \lor gt$, depending on your point of view, of event b. Space Condition: We still need $a$ and $b$ , for time, but also need$x$ and $y$ , for our ships, and then we have to bundle up both ships in the Space condition. So, for any times $a, b$ and ships $x, y$, $if\; a \lt b,\;$ then $S(x_{i}) - S(y_{i}) \langle a \rangle \preccurlyeq S(x_{j}) - S(y_{j}) \langle b \rangle$ 1.1 Summary of results: Mathematics offers the ability to produce the real numbers from primitive notions. Thinking about how quantities are measured, we realize we can define references, with preset amounts, that we then compare to our object, to find some upper and lower bound. A ruler is a series of marks and measuring position with it, means finding the closest tick mark (to said position?). A clock is a similarly performing series of ticks. I just got how time can act like a ruler...and thus get shorter at the speed of light. Thus we understand a quantity is continuous, if, we can compare references ever closer to the quantity.

• References here, seem to be asymptotic(?) here- the limit of the reference point is the quantity (?0_o).

A single reference, allows us to distinguish a before, from and after, which we can then formalize via our notion of a verifiable statement, which we get two of from a reference: The object is before this reference, and the object is after this reference. From this, we can view ordering in a logical sense, where it does not matter if before means along a temporal, or spatial dimension. Quantities themselves, are not a priori objects, but constructions built up from a set of references. A [[Reference Frame]] in space-time thus consists of fixed elements, and the signals exchanged among them, meaning the topology of space-time is an idealized representation of the set of all possible constructions of reference frames, the extent and limitations of which we seek to understand in this paper. We must be careful not to assume that we can use a high resolution than our reference measuring tool, to identify the beginning and end of an object, thus we must only describe relationships and properties logically. From this strategy we get two conclusions: Most conditions are not required by the real numbers, but rather ordered quantities. That is, the set of references have to satisfy only a few conditions, to be sure that the cases they distinguish are ordered. *The conditions are as follows:** References must be strict- before and after cases are mutually exclusive, and if objects have an extent, it must be smaller than the extent of the reference, to be wholly considered before or after the reference. The references must be aligned, meaning their before and after statements identify incremental regions, in short we can always distinguish them, because the before/after relationships are constant. References must be refinable- we should be able to resolve overlaps, such that if an object can be between two references, we should be able to put a reference between the object, and each reference. These are prerequisite for any kind of order (discrete/continuous). The second conclusion is: the inability to distinguish below a certain scale most likely invalidates those conditions. Thus, the points of space time can not be ordered in any meaningful way. To obtain that result, one must simply argue that at least one of the above conditions isn't satisfied. For example: at the finest level the references are particles, and once they become bunched together, it may be impossible to distinguish them from each other, meaning our before/after conditions from earlier are violated. (alignment condition) Alternatively, if both the references and the object being measured are particles, their extent may be comparable, and thus the strictness condition is broken. Finally, as we approach the [[Planck Length]], we may lose the ability to refine our references at some point, violating the refinement condition. Seeing as how we cannot create ordering, we can not define other geometrical quantities, such as angles and distance, therefore, the ultimate structure of space time may very well be topological (or at least must be contemplated as such).